(Picture courtesy of FiveThirtyEight)
If one were to indulge in the scope of NBA analysis, they’d be met by an increasingly large number of methods, ranging from visual to analytic tools. Film study is a relevant, predominant element of modern NBA analysis, and one that when properly wielded can draw strong inferences. However, the foremost option in a player analysis lies in advanced statistics. Despite various suppositions from a subset of questioning individuals, advanced stats are great at estimating a player’s value. They’re widely cited in a broad range of places: social platforms (Discuss TheGame and Instagram) to professional sports analysis and networking (APBRmetrics and ESPN). The widespread trust and utilization in and of advanced stats corroborate the validity of the underlying premises. The succeeding descriptions exist to explicate the calculations and identify the proper use of advanced stats.
[1] Prerequisite Knowledge
The complexity of NBA statistics varies depending on the statistic at hand. Martin Manley’s “Efficiency” (EFF) stat, which measures individual player efficiency, goes as follows:
EFF = [(PTS + TRB + AST + STL + BLK – Missed FG – Missed FT – TO) / GP]
The general grounds of EFF are apparent to most, with positive contributions weighed positively, negative contributions weighed negatively, and the sum eventually adjusted for playing time. The most valid player statistics incorporate more complex subdivisions of mathematics, often superseding traditional arithmetics. To maximize the retention of the formulas for the selected advanced stats, a rudimentary knowledge of linear algebra and regression analysis is highly recommended. The principles of “holy grail” statistics are largely dependent on these two math subdivisions.
To encapsulate the use of matrices and the least-squares solution in advanced stats, the formulation of Adjusted Plus/Minus (APM) will act as the primary step in the manipulation of matrices. Traditional Plus/Minus measures the Net Rating (point differential per 100 possessions) of a given player’s team when he is on the floor. If “Player A” is on the court for twenty possessions and his team outscored the opponent by a single point, “Player A” is credited with a +5 Plus/Minus. Plus/Minus is notoriously biased toward players on great teams playing against inferior competition, as Plus/Minus is insensitive to the quality of teammates surrounding a player and the difficulty of the opposition. Depending on these external factors, a player’s Plus/Minus could either inflate or deflate, straying away from the player’s true value.
The calculation[1] of APM employs an n (number of possessions) x m (number of players involved in the possessions) matrix X. The following step consists of classifying whether a player is on offense, defense, or off the floor with the numerical denotations 1, -1, and 0, respectively. The matrix equation to solve for the beta-values that give the point differential Y goes as follows:
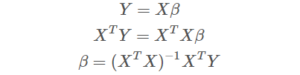
The beta-values are yielded through the least-squares solution, a method used to minimize the sum of square residuals, fitting the data closer to the mean. The approximated β coefficients are players’ APM scores. APM, in theory, is the “holy grail” basketball metric, providing a suppositionally true value score. APM does suffer from phenomena like multicollinearity, begetting the formulation of Regularized Adjusted Plus/Minus (RAPM), which combats the extreme variance in APM and reduces standard errors. As implied through its name, RAPM employs a ridge regression, more specifically an L2 regularization, to reduce variance and center the results from APM. The modification of the least-squares solution to fit the diagonal perturbation matrix λI, a methodology that approximates solutions starting at simpler problems, goes as follows:

The resulting beta-values act as the RAPM scores for players. RAPM garnered recognition as the foremost basketball metric due to its strong foundation and the underlying premise. RAPM isn’t perfect, often taking several years to stabilize, after which the metric was largely taken in three-to-five-year samples. Despite the less positive noise surrounding it, RAPM serves as the base regression for the cream of the crop of one-number metrics. The understanding of RAPM is crucial in also retaining the formulations of its “offspring.”
- Click here to see the RAPM leaders for the current season
- Click here to see the RAPM leaders from a three-year sample
[2] Regression Models
Elementary grasps of regression analysis are additionally applicable in calculating regression models. The bases of several widespread metrics are multiple regressions on multi-year samples of RAPM. NBA Shot Charts is often recognized as the primary RAPM distributor and the most frequent base for an RAPM regression, but similar models (see Jacob Cutter‘s and Simon Zou‘s open-source RAPM models) could also act as strong bases. It’s worth noting the variety of models to determine a player’s RAPM. There isn’t a definitive solution, creating room for a variety of methods. The overarching premise of these stats is to assign coefficients to certain values (box score, On-Off ratings, etc.) based on their correlation to RAPM. These one-number metrics are differentiated based on the chosen values (box score/On-Off ratings, etc.) and the variation/length of the RAPM data set.
Box Plus/Minus (BPM)
Developer: Daniel Myers
Box Plus/Minus consists of a predominant pair of counterparts, provided through Basketball-Reference (Myers’s model) and Backpicks (Ben Taylor’s model). The former includes a detailed description of its methodology and calculation process, two elements the Backpicks model lacks, hence its appearance. BPM estimates the number of points relative to league-average a player contributes every 100 possessions. The statistic is calculated with solely box score values. BPM is based on a twenty-year sample of “Bayesian Era” RAPM, which uses a prior probability distribution that considers team quality and minutes per game in its seasons. The regression includes sets of coefficients for cumulative BPM and its offensive half (OBPM), with variances based on position (e.g. steals are weighed more for centers than point guards due to positional difficulties). BPM builds on the regression coefficients with a series of adjustments based on team quality (in BPM and OBPM) and position. Multiple regression coefficients typically remain stagnant due to optimized data, but BPM’s weaker correlation to RAPM (compared to other one-number metrics) allows for more flexibility in adjustments.
BPM is limited by a solely box-oriented calculation but remains one of the stronger metrics in player analysis. Retrodiction testing, the process of predicting team equity (in Simple Rating System (SRS)) based on a rosters’ players’ previous stats, paints it as on par with play-by-play informed stats. From 1978 to 2019, compared to Win Shares, Backpicks BPM, and Player Impact Plus/Minus (PIPM), BPM had an SRS error (the absolute difference between predicted and actual SRS) of approximately 3.8 with a lineup continuity (the percent of the remaining roster from the previous year) of 60% (third) and an SRS error of approximately 2.5 with a lineup continuity of 95% (first), solidifying its status as a highly indicative stat. BPM’s predictive power transcends its descriptive power, however. Its descriptiveness is summarized through its Pearson correlation to RAPM, which stands at a rounded 0.66[2]. Despite restrictions due to an exclusively box-score formulation, BPM serves mostly well as an indicator of player value, and an even stronger prospective evaluation.
- Click here to see an in-depth overview of Box Plus/Minus
- Click here to see a walk-through calculation of Box Plus/Minus
Robust Algorithm using Player Tracking and On/Off Ratings (RAPTOR)
Developer: FiveThirtyEight
FiveThirtyEight‘s “RAPTOR” metric is the newest of the popular one-number metrics (released in October of 2019), but makes a case as the most descriptive and predictive. The site previously employed an Elo-based projection that garnered a reputation as one of the most accurate NBA projection models, most notably predicting the Toronto Raptors’ championship run last season. FiveThirtyEight implied it created the RAPTOR metric for one overarching reason: modernization. RAPTOR employs more modern NBA data (player tracking and play-by-play) and models the preferences of NBA teams. The stat only uses data available to the public. RAPTOR measures the number of points relative to league-average a player contributes per 100 possessions. RAPTOR is based on a six-year RAPM sample, including components from an expanded box score and luck-adjusted On-Off ratings. Evidently, the coefficients for the enhanced elementary stats are determined through the aforementioned regression, which was based on a six-year sample of RAPM. The predictive power of RAPTOR hasn’t yet been tested, but the metric serves as the foundation of FiveThirtyEight‘s projection model. Although denoted as a descriptive stat, RAPTOR’s correlation to the base regression isn’t explicitly stated. The premise of RAPTOR is inherently strong, and time will tell the individual proficiencies and deficiencies of the metric.
Real Plus/Minus (RPM)
Developers: Jeremias Engelmann / Steve Ilardi
Real Plus/Minus, the featured statistic of ESPN, is similarly modeled to the preceding statistics in BPM and RAPTOR. The base regression is on a set of xRAPM (Engelmann’s RAPM model) to estimate a player’s contributions on the offensive and defensive ends in a Net point differential. RPM is the most exclusively engineered statistic among the widespread set, with little to no light shed on its calculations. The stat is most noted for its predictive power, acting as the driving force of ESPN‘s NBA projections. If one were to make suppositions of RPM, it may consist of a variety of points. Engelmann, the co-developer of RPM as well as xRAPM, garners a strong reputation for building world-class valuation models, and the assumption that RPM likely holds a high Pearson correlation to xRAPM is rational. The number is an estimated 0.71[3], making it of statistical significance against RAPM. RPM is as proprietary as a publicly-available metric could be. Ideally, a more informed methodology and rough calculation would be published. Limited validity testing is available to determine the numerical equity of the stat. However, due to the developer, distributor, and the given premise of RPM, it’s a foremost citation to estimate player value.
Player Impact Plus/Minus (PIPM)
Developer: Jacob Goldstein
Player Impact Plus/Minus is the primary impact metric of Basketball Index. PIPM estimates the number of points a player contributes on offense and defense per 100 possessions, mirroring its predecessors. The stat employs two similar components to RAPTOR: an expanded box score and luck-adjusted On-Off ratings. The box-score prior and On-Off ratings incorporate “pace-adjusted per 36 minutes” stats and relative luck-adjusted On-Off ratings, respectively. Although it’s not explicitly stated, it could be inferred the “luck-adjusted” component of the On-Off ratings accounts for team and opponent context: the quality of teammates and opposition, perhaps. Luck adjustments in these contexts also relate to a player’s unexpected progressions or regressions, for which career numbers are substituted (a concept used in luck-adjusted RAPM). The former may have more likelihood, but either description is possible. The coefficients for PIPM were determined through a regression on a fifteen-year sample of Engelmann’s RAPM. PIPM holds unprecedented accuracy, maintaining a Pearson correlation of 0.875 to the base regression. The communal precision of PIPM creates one of, if not, the foremost metrics in player analysis.
PIPM’s validity is maintained in retrodiction testing. As a part of the initial group of tested metrics stated earlier, PIPM held the lowest SRS error between 60% and 90% lineup continuity, permitting a marginal difference to Box Plus/Minus nearing 95%. The evidence suggesting PIPM’s clarity makes it a contender for the most valid one-number metric in the NBA.
- Click here to see an in-depth overview of PIPM
- Click here to see seasonal and multi-year PIPM leaders
[3] Conclusion
The premises of the aforementioned statistics – BPM, RAPTOR, RPM, and PIPM – imply an important principle: metrics are great indicators of player value. The term “value” initially garnered negative noise as it was generally used in a situational context, but the establishments of these one-number metrics created the “isolated” value measurements. They account for the quality of teammates and opponents to confidently estimate player impact on a leveled playing field. These ideas have been expanded on to create the concepts of portability (how well a player’s skills scale alongside great teammates) and diminishing returns (lessened situational value alongside greater teammates). Advanced statistics clear a lot of noise around traditional stats, introducing analytic concepts and new calculation approaches to (very precisely) estimate a player’s value. Advanced statistics will remain a principal tool in player analysis, and a firm grasp of their processes and measurements is a fundamental step in analytic retention.
Leave a Reply